已知函數(shù)f(x)的定義域為[-1,5],部分對應(yīng)值如下表.f(x)的導(dǎo)函數(shù)y=f′(x)的圖象如圖所示.
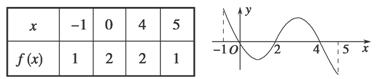
下列關(guān)于函數(shù)f(x)的命題:
①函數(shù)y=f(x)是周期函數(shù)����;
②函數(shù)f(x)在[0,2]上是減函數(shù)����;
③如果當(dāng)x∈[-1���,t]時,f(x)的最大值是2���,那么t的最大值為4���;
④當(dāng)1<a<2時,函數(shù)y=f(x)-a有4個零點.
其中真命題的個數(shù)有 ( ).
A.4 B.3 C.2 D.1