相關習題
0 147339 147347 147353 147357 147363 147365 147369 147375 147377 147383 147389 147393 147395 147399 147405 147407 147413 147417 147419 147423 147425 147429 147431 147433 147434 147435 147437 147438 147439 147441 147443 147447 147449 147453 147455 147459 147465 147467 147473 147477 147479 147483 147489 147495 147497 147503 147507 147509 147515 147519 147525 147533 266669
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試浙江卷數(shù)學理科
題型:044
如圖�,在四棱錐P-ABCD中�����,底面是邊長為2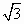 的菱形��,且∠BAD=120°����,且PA⊥平面ABCD����,PA=2
的菱形��,且∠BAD=120°����,且PA⊥平面ABCD����,PA=2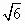 ���,M,N分別為PB��,PD的中點.
���,M,N分別為PB��,PD的中點.
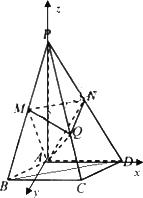
(Ⅰ)證明:MN∥平面ABCD�;
(Ⅱ)過點A作AQ⊥PC,垂足為點Q���,求二面角A-MN-Q的平面角的余弦值.
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試浙江卷數(shù)學理科
題型:044
已知箱中裝有4個白球和5個黑球�,且規(guī)定:取出一個白球的2分�,取出一個黑球的1分.現(xiàn)從該箱中任取(無放回,且每球取到的機會均等)3個球��,記隨機變量X為取出3球所得分數(shù)之和.
(Ⅰ)求X的分布列�;
(Ⅱ)求X的數(shù)學期望E(X).
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試浙江卷數(shù)學理科
題型:044
在△ABC中,內(nèi)角A�����,B��,C的對邊分別為a�����,b,c.已知cosA=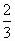 ��,sinB=
��,sinB=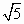 cosC.
cosC.
(Ⅰ)求tanC的值�;
(Ⅱ)若a=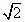 ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
設集合Pn={1����,2,…���,n}�����,n∈N+.記f(n)為同時滿足下列條件的集合A的個數(shù):
①A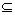 Pn�����;
Pn�����;
②若x∈A�,則2x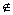 A���;
A���;
③若x∈ A,則2x
A,則2x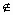
 A.
A.
(1)求f(4)�����;
(2)求f(n)的解析式(用n表示).
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
設ξ為隨機變量,從棱長為1的正方體的12條棱中任取兩條����,當兩條棱相交時,ξ=0�;當兩條棱平行時,ξ的值為兩條棱之間的距離��;當兩條棱異面時ξ=1.
(1)求概率p(ξ=0)
(2)求ξ的分布列���,并求其數(shù)學期望E(ξ).
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
[選修4-1:幾何證明選講]
如圖��,AB是圓O的直徑���,D,E為圓O上位于AB異側(cè)的兩點��,連結(jié)BD并延長至點C���,使BD=DC�����,連結(jié)AC���,AE,DE.
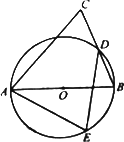
求證:∠E=∠C.
已知矩陣A的逆矩陣A-1=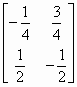 �����,求矩陣A的特征值.
�����,求矩陣A的特征值.
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
如圖����,在平面直角坐標系xOy中��,橢圓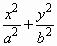 =1(a>b>0)的左�����、右焦點分別為F1(-c���,0)����,F(xiàn)2(c�����,0).已知(1,e)和(e����,
=1(a>b>0)的左�����、右焦點分別為F1(-c���,0)����,F(xiàn)2(c�����,0).已知(1,e)和(e����,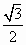 )都在橢圓上,其中e為橢圓的離心率.
)都在橢圓上,其中e為橢圓的離心率.
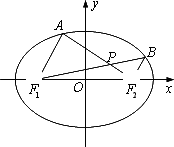
(1)求橢圓的離心率�;
(2)設A,B是橢圓上位于x軸上方的兩點��,且直線AF1與直線BF2平行�,AF2與BF1交于點P.
(i)若AF1-BF2=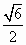 ,求直線AF1的斜率��;
,求直線AF1的斜率��;
(ii)求證:PF1+PF2是定值.
查看答案和解析>>
科目:
來源:2012年普通高等學校招生全國統(tǒng)一考試江蘇卷數(shù)學
題型:044
已知a��,b是實數(shù)��,1和-1是函數(shù)f(x)=x3+ax2+bx的兩個極值點.
(1)求a和b的值��;
(2)設函數(shù)g(x)的導函數(shù) (x)=f(x)+2�,求g(x)的極值點;
(x)=f(x)+2�,求g(x)的極值點;
(3)設h(x)=f(f(x))-c����,其中c∈[-2,2],求函數(shù)y=h(x)的零點個數(shù).
查看答案和解析>>
