相關習題
 0  140875  140883  140889  140893  140899  140901  140905  140911  140913  140919  140925  140929  140931  140935  140941  140943  140949  140953  140955  140959  140961  140965  140967  140969  140970  140971  140973  140974  140975  140977  140979  140983  140985  140989  140991  140995  141001  141003  141009  141013  141015  141019  141025  141031  141033  141039  141043  141045  141051  141055  141061  141069  366461 

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

某地區(qū)林業(yè)局要考察一種樹苗移植的成活率，對該地區(qū)這種樹苗移植成活情況進行調查統(tǒng)計，并繪制了如圖所示的統(tǒng)計表，根據統(tǒng)計圖提供的信息解決下列問題：
（1）這種樹苗成活的頻率穩(wěn)定在______，成活的概率估計值為______．
（2）該地區(qū)已經移植這種樹苗5萬棵．
①估計這種樹苗成活______萬棵；
②如果該地區(qū)計劃成活18萬棵這種樹苗，那么還需移植這種樹苗約多少萬棵？

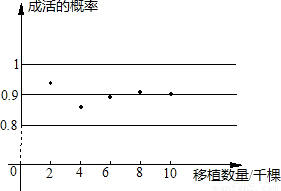
查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

一只不透明的袋子中裝有4個小球，分別標有數字2，3，4，x，這些球除數字外都相同．甲、乙兩人每次同時從袋中各隨機摸出1個球，并計算摸出的這2個小球上數字之和．記錄后都將小球放回袋中攪勻，進行重復實驗．實驗數據如下表：解答下列問題：
（1）如果實驗繼續(xù)進行下去，根據上表數據，出現(xiàn)“和為7”的概率將穩(wěn)定在它的概率附近，試估計出現(xiàn)“和為7”的概率；
（2）根據（1），若x是不等于2，3，4的自然數，試求x的值．
 摸球總次數 1020  30 60 90 120 180 240330 450 
“和為7”出現(xiàn)的頻次 1 9 14 24 26 3758 82 109 150
“和為7”出現(xiàn)的頻率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

某校九年級一班的暑假活動安排中，有一項是小制作評比．作品上交時限為8月1日至30日，班委會把同學們交來的作品按時間順序每5天組成一組，對每一組的件數進行統(tǒng)計，繪制成如圖所示的統(tǒng)計圖．已知從左到右各矩形的高度比為2：3：4：6：4：1．第三組的頻數是12．請你回答：
（1）本次活動共有______件作品參賽；
（2）上交作品最多的組有作品______件；
（3）經評比，第四組和第六組分別有10件和2件作品獲獎，那么你認為這兩組中哪個組獲獎率較高？為什么？
（4）對參賽的每一件作品進行編號并制作成背面完全一致的卡片，背面朝上的放置，隨機抽出一張卡片，抽到第四組作品的概率是多少？

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共40個，小穎做摸球實驗，她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色，再把它放回盒子中，不斷重復上述過程，下表是實驗中的一組統(tǒng)計數據：
摸球的次數n10020030050080010003000
摸到白球的次數m651241783024815991803
摸到白球的頻率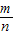0.650.620.5930.6040.6010.5990.601
（1）請估計：當n很大時，摸到白球的頻率將會接近______；（精確到0.1）
（2）假如你摸一次，你摸到白球的概率P（白球）=______；
（3）試估算盒子里黑、白兩種顏色的球各有多少只？

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

某活動小組為了估計裝有5個白球和若干個紅球（每個球除顏色外都相同）的袋中紅球接近多少個，在不將袋中球倒出來的情況下，分小組進行摸球試驗，兩人一組，共20組進行摸球實驗．其中一位學生摸球，另一位學生記錄所摸球的顏色，并將球放回袋中搖勻，每一組做400次試驗，匯總起來后，摸到紅球次數為6000次．
（1）估計從袋中任意摸出一個球，恰好是紅球的概率是多少？
（2）請你估計袋中紅球接近多少個？

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

一粒木質中國象棋子“兵”，它的正面雕刻一個“兵”字，它的反面是年平的．將它從一定高度下擲，落地反彈后可能是“兵”字面朝上，也可能是“兵”字面朝下．由于棋子的兩面不均勻，為了估計“兵”字面朝上的概率，某實驗小組做了棋子下擲實驗，實驗數據如下表：
實驗次數20406080100120140160
“兵”字面朝上頻數14384752667888
相應頻率0.70.450.630.590.520.560.55
（1）請將數據補充完整；
（2）畫出“兵”字面朝上的頻率分布折線圖；

（3）如果實驗繼續(xù)進行下去，根據上表的數據，這個實驗的頻率將穩(wěn)定在它的概率附近，請你估計這個概率是多少？

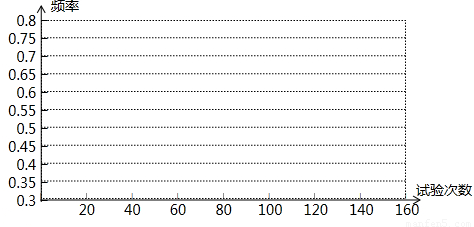
查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

小穎和小紅兩位同學在學習“概率”時，做投擲骰子（質地均勻的正方體）實驗，他們共做了60次實驗，實驗的結果如下：
朝上的點數123456
出現(xiàn)的次數79682010
（1）計算“3點朝上”的頻率和“5點朝上”的頻率．
（2）小穎說：“根據實驗，一次實驗中出現(xiàn)5點朝上的概率最大”；小紅說：“如果投擲600次，那么出現(xiàn)6點朝上的次數正好是100次．”小穎和小紅的說法正確嗎？為什么？
（3）小穎和小紅各投擲一枚骰子，用列表或畫樹狀圖的方法求出兩枚骰子朝上的點數之和為3的倍數的概率．

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

在一個不透明的口袋里裝有只有顏色不同的黑、白兩種顏色的球共20只，某學習小組做摸球實驗，將球攪勻后從中隨機摸出一個球記下顏色，再把它放回袋中，不斷重復．下表是活動進行中的一組統(tǒng)計數據：
摸球的次數n1001502005008001000
摸到白球的次數m5896116295484601
摸到白球的頻率0.580.640.580.590.6050.601
（1）請估計：當n很大時，摸到白球的頻率將會接近______；
（2）假如你去摸一次，你摸到白球的概率是______，摸到黑球的概率是______；
（3）試估算口袋中黑、白兩種顏色的球各有多少只？
（4）解決了上面的問題，小明同學猛然頓悟，過去一個懸而未決的問題有辦法了．這個問題是：在一個不透明的口袋里裝有若干個白球，在不允許將球倒出來數的情況下，如何估計白球的個數（可以借助其他工具及用品）請你應用統(tǒng)計與概率的思想和方法解決這個問題，寫出解決這個問題的主要步驟及估算方法．

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

王強與李剛兩位同學在學習“概率”時．做拋骰子（均勻正方體形狀）實驗，他們共拋了54次，出現(xiàn)向上點數的次數如下表：
向上點數123456
出現(xiàn)次數69581610
（1）請計算出現(xiàn)向上點數為3的頻率及出現(xiàn)向上點數為5的頻率；
（2）王強說：“根據實驗，一次試驗中出現(xiàn)向上點數為5的概率最大．”李剛說：“如果拋540次，那么出現(xiàn)向上點數為6的次數正好是100次．”請判斷王強和李剛說法的對錯；
（3）如果王強與李剛各拋一枚骰子．求出現(xiàn)向上點數之和為3的倍數的概率．

查看答案和解析>>

科目： 來源：第23章《概率的求法與應用》中考題集（27）：23.1 求概率的方法（解析版） 題型：解答題

為了調查淮安市今年有多少名考生參加中考，小華從全市所有家庭中隨機抽查了200個家庭，發(fā)現(xiàn)其中10個家庭有子女參加中考．
（1）本次抽查的200個家庭中，有子女參加中考的家庭的頻率是多少？
（2）如果你隨機調查一個家庭，估計該家庭有子女參加中考的概率是多少？
（3）已知淮安市約有1.3×106個家庭，假設有子女參加中考的每個家庭中只有一名考生，請你估計今年全市有多少名考生參加中考？

查看答案和解析>>

同步練習冊答案